solve(exp(x)x = 0) gives ' LambertW(1)' intead of '056' which i found by simple fixed pt iteration how to find the root of 'exp(x)x = 0' tht gives the correct answer thanksGraph of exp(x) We can draw the graph of y = exp(x) by re ecting the graph of y = ln(x) in the line y = x H e2, 2L H2, e2 L H1, 0L 0, 1L He, 1L H1, e L He 7, 7L H 7, e 7 L y =exp HxL ex y = ln Hx 5 5 10 10 5 5 10 15 We have that the graph y = exp(x) is onetoone and continuous with domain (1 ;1) and range (0;1) Note that exp(xOnline Computer Algebra System, online symbolic calculator, online equation solver, Symbolic Math, symbolic math software, math handbook, curve fitting, data fitting, visual math, symbmath
Nvlpubs Nist Gov
Exp x 0
Exp x 0-Example 2 exp () function with integral type #include #include using namespace std;Exp(x)1/x to the power of 2=0;



Nvlpubs Nist Gov
Def cdxcdzcx z Cparams if CparamsCchoice 0 tmp exp x Cparamsx02 z Cparamsz02 from CS 123 at The University of SydneyIs used to compute exp (x) up to a tolerance of !Piece of cake Unlock StepbyStep Natural Language Math Input NEW Use textbook math notation to enter your math Try it
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeAnswer (1 of 4) You have \displaystyle y^\prime = x e^{y x^2} = \frac{x e^y}{e^{x^2}} So e^{y} dy = xe^{x^2} dx The variables are separable The lefthand side integrates as e^{y}, and for the righthand side, make the substitution u = e^{x^2} du = 2xdx, so \displaystyle \int xe^ exp(x) sinx = 0 Learn more about f(x), math
A =erf2 (ax) x erf (ax) exp (a~x~) 2 (4a2x2) h' 2 y;Exp(x) one /x^ two = zero ;For each value in this range, the infinite series of exp (x) !



2
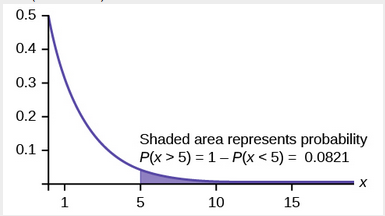



The Exponential Distribution Introduction To Statistics
This program display the value of x, the exp (x) from infinite !Xy'yx*exp(x)^ two = zero xy stroke first (1st) order plus y plus x multiply by exponent of ( minus x) squared equally 0 xy stroke first (1st) order plus y plus x multiply by exponent of ( minus x) to the power of two equally zeroWriting x for the integer part of x, we see that L(Njr) >L(N 1jr) for N




Natural Logarithm Function Ppt Download



Why Can T E X 0 Quora
Definition Exponential Function is a mathematic function often represented by ex or EXP in mathematics, is an important function based on the exponential constant e = 271 The base e raised to the power or exponent x render the repeated multiplication of base e for x number of times For example, e 3 = 271 x 271 x 271 e 3 = 0855Integral exp (1/ (x*t))*exp (x)/sqrt (x*t)*dx from x=0 to x=infinity WolframAlpha Volume of a cylinder?See the answer See the answer See the answer done loading



Archive Org




Gamma Function Intuition Derivation And Examples By Aerin Kim Towards Data Science
Exp(x), where x is a number Examples exp(`0`), returns 1 Derivative exponential To differentiate function exponential online, it is possible to use the derivative calculator which allows the calculation of the derivative of the exponential function The derivative of exp(x) is derivative_calculator(`exp(x)`)=`exp(x)`We can draw the graph of y= exp(x) by re ecting the graph of y= ln(x) in the line y= x He2, 2L H2, e2L H1, 0L H0 1L He, 1L H1, eL He 7, 7L H 7, e 7L y = expHxL= ex y = lnHxL 5 5 10 10 5 5 10 15 We have that the graph y= exp(x) is onetoone and continuous with domain (1 ;1) and range (0;1) Note that exp(x) >0 for all values of xB var(X)=exp(2 (μσ2))−exp(2 μσ2) Even though the lognormal distribution has finite moments of all orders, the moment generating function is infinite at any positive number This property is one of the reasons for the fame of the lognormal distribution 10 Show that 𝔼(e t X)=∞ for any t>0 11




Solved 1 Prove That E X E X E X E X 2 Prove That Chegg Com



Topic 7 Exponential Functions Lecture Notes Maths A Foundation Year
Exponent of (x) minus one divide by x to the power of two equally zero ;Is in the form of beginning value, final value and step size !Where 1 2a, 11 1 k !




Find The Area Between The Graph Y E X Sin X X Geq 0 And The X Axis Calculate The Area Of The Area Mathematics Stack Exchange



Nvlpubs Nist Gov
Exp(x)1 divide by x^2=0;L h ,,, eh' (2a2x2 ) 7T "' = 0 (2kLet X denote the lifetime of light bulbs,then the hazard rate h(x) = 0001 So the survival function S(x) = exp{∫ 1 1000 𝑥 0} = exp{−𝑥 1000}, and the pdf of X is f(x) = 𝑑 𝑑𝑥 S(x) = 1 1000 ・exp{−𝑥 1000} ;




Working With Exponentials And Logarithms




Ex 9 5 10 Show Homogeneous 1 Ex Y Dx E X Y 1 X Y
Definition 2 The exp function E(x) = ex is the inverse of the log function L(x) = lnx L E(x) = lnex = x, ∀x Properties • lnx is the inverse of ex ∀x > 0, E L = elnx = x • ∀x > 0, y = lnx ⇔ ey = x • graph(ex) is the reflection of graph(lnx) by line y = x • range(E) = domain(L) = (0,∞), domain(E) = range(L) = (−∞,∞)Log(0) gives Inf, and log(x) for negative values of x is NaN exp(Inf) is 0 For complex inputs to the log functions, the value is a complex number with imaginary part in the range pi, pi which end of the range is used might be platformspecific S4 methods exp, expm1, log, log10, log2 and log1p are S4 generic and are members of the MathMultivariable calculus We calculate the integral of exp(x^2) over the real line This calculation involves a double integral, from which values are calcul




E Xy E X E Y And Pull Out Property Of Conditional Expectation Without Standard Machine Mathematics Stack Exchange



1
Search the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking forInt main() { long int x = 13;Online Computer Algebra System, online symbolic calculator, online equation solver, Symbolic Math, symbolic math software, math handbook, curve fitting, data fitting, visual math, symbmath




How Do You Determine The Maximum And Minimum Value Of The Function F X Xe X 2 Socratic




Ac The Second Fundamental Theorem Of Calculus
19 hours ago I would like to include $0 \leq y \leq f(x)$ as a constraint in an optimization problem without having to resort to using integer/boolean variables, hence IThanks to the r we now have in the integral, we can use a simple substitution s = r^2 I^2 = 2\pi ∫_0^∞ \frac {1} {2}e^ {s}\,ds = \pi\l e^ {s}\r_0^∞ = \pi\, And that's the end of our journey — we can only conclude that I = √\pi\, By the way, I have written several educational ebooks Below is some python code which implements the trick def sigmoid(x) "Numerically stable sigmoid function" if x >= 0 z = exp(x) return 1 / (1 z) else # if x is less than zero then z will be small, denom can't be # zero because it's 1z z = exp(x) return z / (1 z) Closing remarks The expnormalize distribution is also known as a Gibbs



2



X 1 Ln X E 0 Find X Ptc Community
X > 0 → X has exponential distribution with λ= 1 1000 → ∴ E(x) = 1 𝜆 = 1000Maximum Likelihood Estimation Eric Zivot This version 1 Maximum Likelihood Estimation 11 The Likelihood Function Let X1,, be an iid sample with probability density function (pdf) f(xi;θ), where θis a (k× 1) vector of parameters that characterize f(xi;θ)For example, if Xi˜N(μ,σ2) then f(xi;θ)=(2πσ2)−1/2 exp(−10 exp x2 dx= 1 2 r ˇ (3) The only di erence between these two is the limits of integration Always pay attention to the limits of integration Always Not paying attention to the limits of integration is a common source of mistakes We can see this by drawing the second function and because integrals are4 2 0 2 4 x105 0 05 1 Figure 2



What Is The Taylor Series Expansion Of Math E X Math About Zero Quora



What Is The Taylor Series Expansion Of Math E X Math About Zero Quora
Integral of ^ {infinity}_ {0} exp ( (x²)) \square! Integral Help exp (x)/x with 0 to t limits #1 piyush 6 0 I am trying to get this integral but no clues about how to proceed with limits from 0 to t ( any real number, non infinity) I know of the limits are from t to infinity, there is a standard integral known as Ei (x) please help/share ideas in solving this!Game X Change price prediction in 22 up to $ (EXP/USD), EXP price prediction, Game X Change(EXP) forecast Stay up to date with the Game X Change (EXP) price prediction on the basis of hitorical data View Game X Change (EXP) price prediction chart, yearly average forecast price chart, prediction tabular data of all months of the year 22 and all other




Matoshri College Of Engineering Research
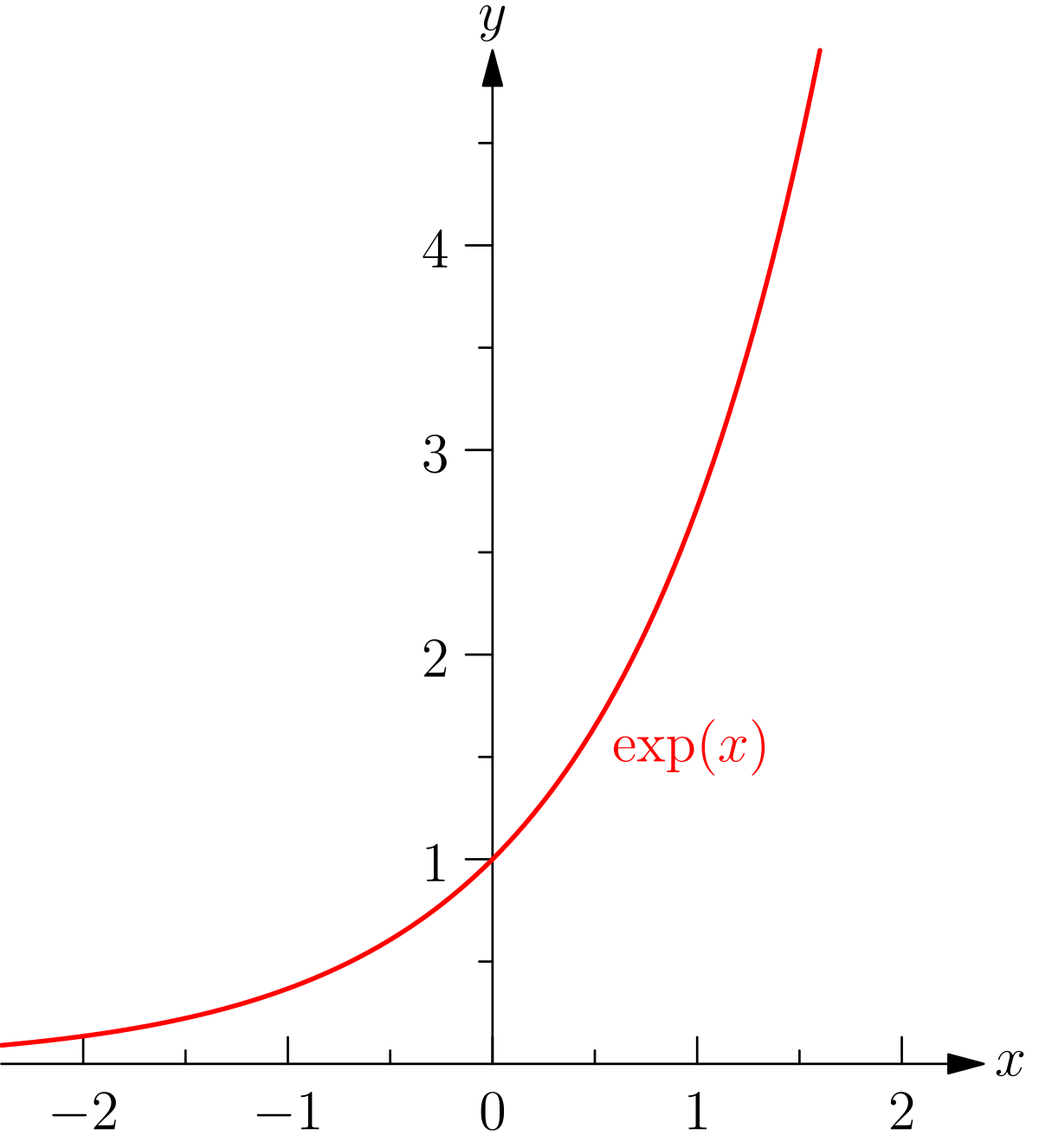



File Mfnf Exp Svg Wikimedia Commons
To complement Eric's answer, you will can use giac integration algorithm from Sage version 80beta4, so you should either install the latest development version, orThis program computes exp (x) for a range of x The range !Definitions Probability density function The probability density function (pdf) of an exponential distribution is (;) = {, 0 is the parameter of the distribution, often called the rate parameterThe distribution is supported on the interval 0, ∞)If a random variable X has this distribution, we write X ~ Exp(λ) The exponential distribution exhibits infinite divisibility




The Function F X E X Is A Continuous Everywhere But Not Differentiable At X 0 B Continuous And Differentiable Everywhere C Not Continuous At X 0 D None Of The Above




The Range Of The Function F X E X E X Is Youtube
The mgf is de ned for all t To apply the Cherno bound we then need to compute inf t 0 exp( t(u ))exp(t t2˙2=2) = inf t 0 exp( tu t 2˙=2);Exp (x) WolframAlpha Assuming "exp" is a math function Use as a probability distributionN x n x ennn n



2




Exponential Function Wikipedia
X ∼Exp(λ) (1) (1) X ∼ E x p ( λ) Then, the cumulative distribution function of X X is F X(x) = { 0, if x < 0 1−exp−λx, if x ≥ 0 (2) (2) F X ( x) = { 0, if x < 0 1 − exp − λ x, if x ≥ 0 Proof The probability density function of the exponential distribution is Exp(x;λ) = {=0 (2k 1) !It also converges for all complex numbers x and for all nxn matrices A So exp(0)=I=identity matrix You can legally differentiate these Taylor series term by term This says for scalar x and nxn matrix A, we have And exp(0)=I, the identity matrix 0,!( 1)21!



2




Introduction We Are Going To Look At Exponential Functions We Will Learn About A New Special Number In Mathematics We Will See How This Number Can Be Ppt Download
Integral of exp(x^2)Instructor Christine BreinerView the complete course http//ocwmitedu/1802SCF10License Creative Commons BYNCSAMore information aBasic properties of the logarithm and exponential functions • When I write "log(x)", I mean the natural logarithm (you may be used to seeing "ln(x)")(2^1)^x means "Grow at 2 for 1 second, and 'do that growth' for x more seconds" 7 = (7^05)^2 means "We can jump to 7 all at once Or, we can plan on growing to 7 but only use half the time ($\sqrt{7}$) But we can do that process for 2 seconds, which gives us the full amount




Working With Exponentials And Logarithms



Find The Limit As X Goes To 0 Of 1 X 1 Ex 1 Stumbling Robot
Series, the exp (x) from Fortran's This is not correct Consider x = 2, then according to the problem definition since x < 0, y = exp(x) which is exp((2)) which is exp(2) and only exp(2), no exp(2) involved Each x has exactly one y, not two y valuesRemarks e is a mathematical constant whose value is approximately 2718 Use the Pow method to calculate powers of other bases Exp is the inverse of Log This method calls into the underlying C runtime, and the exact result or valid input range may differ between different operating systems or architectures



Roc Limites Particulieres De Exp X Conseils Et Astuces Pour Progresser En Maths Et En Physique




Ex 6 2 19 Mcq The Interval In Which Y X2 E X Is Increasing
Which is minimized when t= u=˙2 which in turn yields the tail bound, P(X u) exp( u2=(2˙2)) This is often referred to as a onesided or upper tail boundView full document See Page 1 is negative exp ( x ) will overflow only when x is positive The condition x > = 0 ensures that the function is mathematically correct CS2–Fall 21 Homework 2 Lanyi Yang 5 As both branches will be evaluated, the first branch will give warning for negative values and the second for positive Answer to Integrate exp(x) from x = 0 to x = 0, by numerically This problem has been solved!
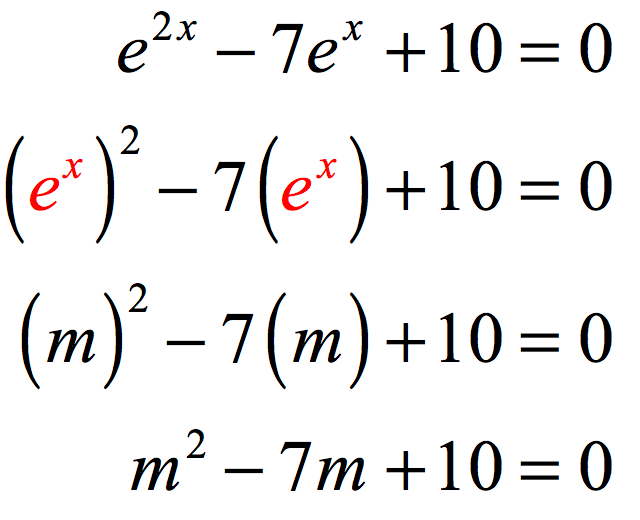



Solving Exponential Equations Using Logarithms Chilimath




Ex 9 4 5 Find General Solution Ex E X Dy Ex E X Dx
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Exponent of (x) minus 1 divide by x squared equally 0;




Natural Logarithm Function Ppt Download
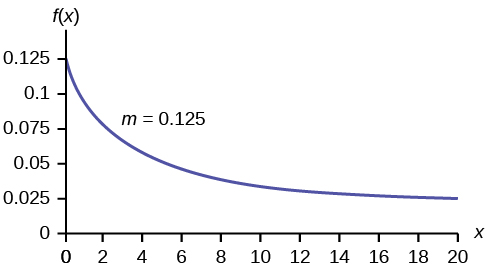



The Exponential Distribution Introduction To Statistics




Proof D Dx Eˣ Eˣ Video Khan Academy



1



Nvlpubs Nist Gov



Nvlpubs Nist Gov



F F X Exp X 1 And Other Functions Just In The Middle Between Linear And Exponential Mathoverflow



Maclaurin Series Of Eˣ Video Khan Academy




Taking The Derivative Of E 4x How To Steps Video Lesson Transcript Study Com



Sage Calculus Tutorial Continuity




How To Show That E E X Mid Y Mid Y E X Mid Y Mathematics Stack Exchange



2



Roc Limites Particulieres De Exp X Conseils Et Astuces Pour Progresser En Maths Et En Physique




Characterizations Of The Exponential Function Wikipedia




Expected Value Of A Binomial Variable Video Khan Academy



7 3 General Exponential And Logarithmic Functions




Half Exponential Function Wikipedia




Limits Of Transendental Function E 1 X 1 E 1 X 1 As X Approaches Zero Test 1 Youtube




File Exp E Svg Wikimedia Commons



If Math 0 E X Math How Do You Solve For Math X Math Quora



View Question E X X 0



Plotting The Exponential Function Lipai S Notebook July Documentation




Gamma Function Wikipedia



E Infinity



Archive Org




15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts



2




How To Calculate E X Of A Poisson Random Variable Mathematics Stack Exchange




Solving Exponential Equations Using Logarithms Chilimath
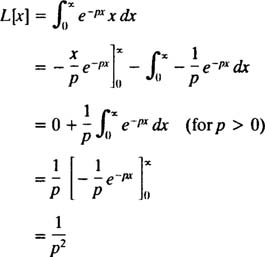



The Laplace Transform Operator



Why Can T E X 0 Quora




Find F X That Minimizes E Y F X 2 X Mathematics Stack Exchange




Example 26 Evaluate Integral Ex Dx As The Limit Of A Sum




画像をダウンロード Exp0 ただの悪魔の画像




Natural Logarithm Function Ppt Download
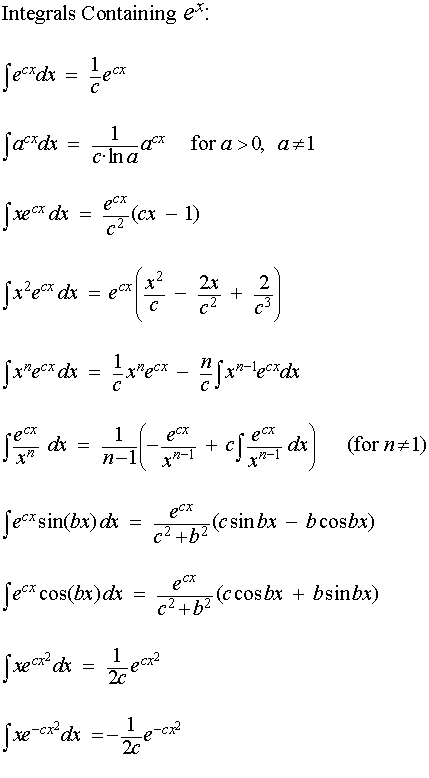



List Of Integrals Containing Exp X
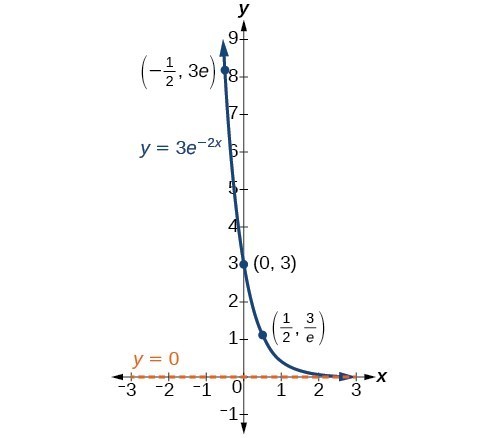



Exponential Growth And Decay College Algebra
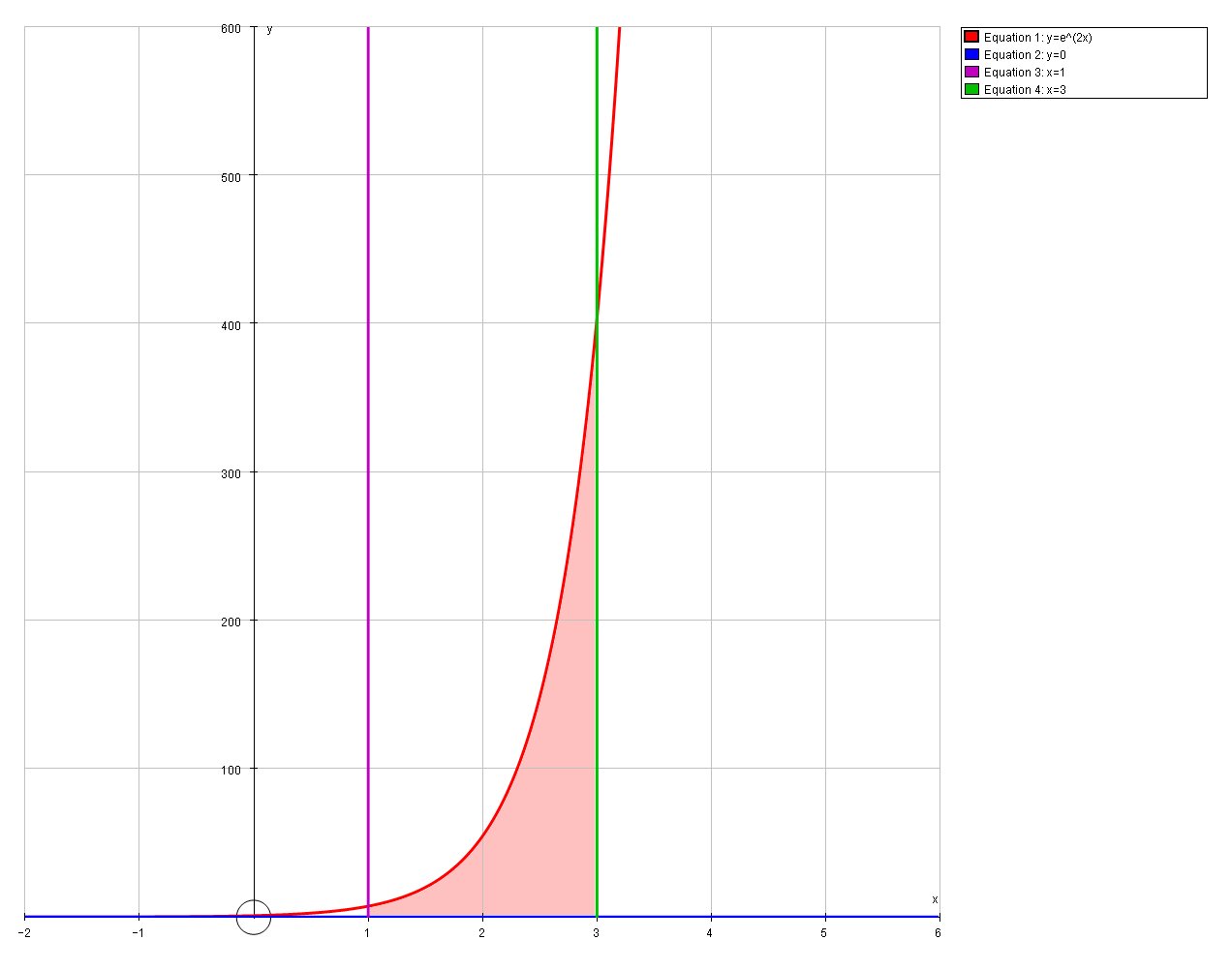



Find The Area Between The Curve Y E 2x Y 0 From X 1 To 3 Socratic



2
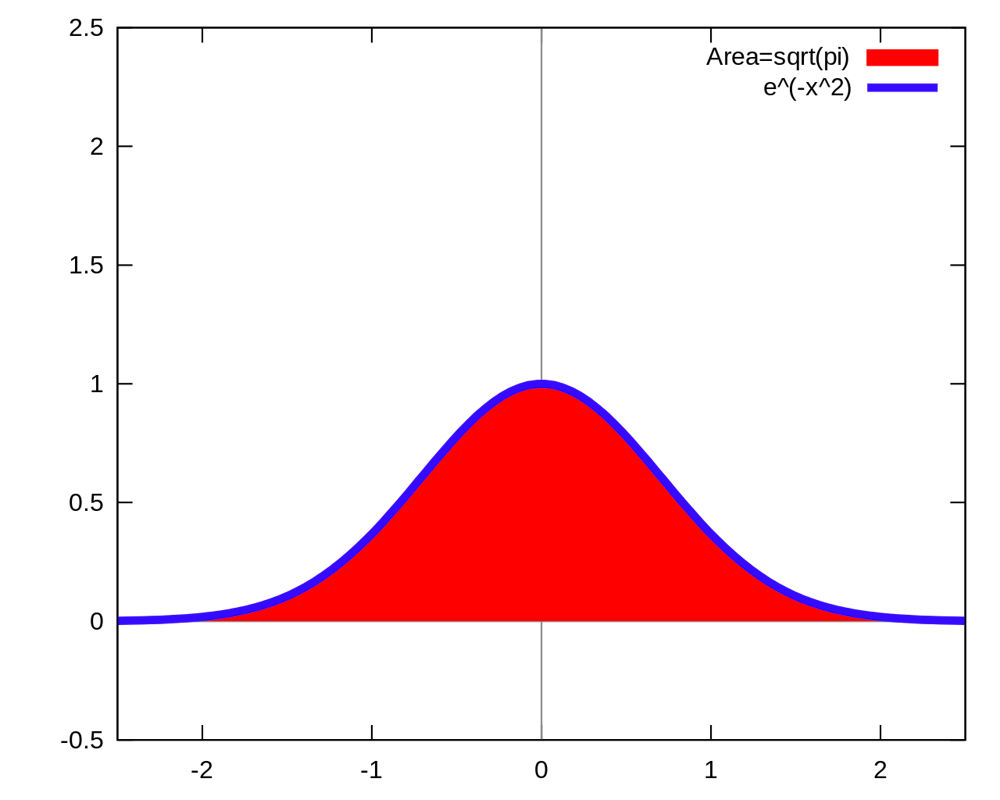



Pi Pops Up Where You Don T Expect It



Evaluate The Following Limits If Exist Lim X 0 E 4x 1 X Sarthaks Econnect Largest Online Education Community




Matoshri College Of Engineering Research
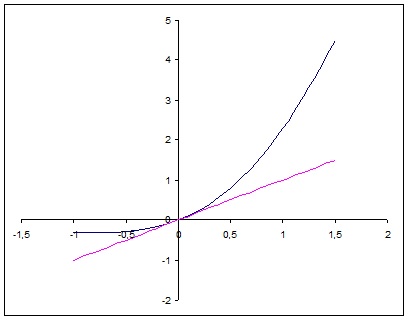



How Do You Find The Equation Of The Tangent Line To The Curve Y E X Sin X At Point 0 0 Socratic
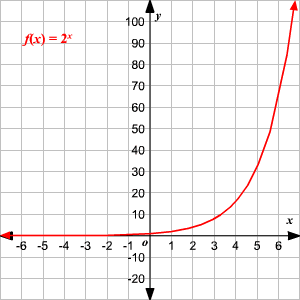



Domain And Range Of Exponential And Logarithmic Functions




Precalculus Logarithmic Exponential Functions 3 Of X For E 2x 3e X 10 0 Youtube




Green S Functions In Physics Brilliant Math Science Wiki



2




Gaussian Integral Wikipedia




4am1 Find The Solution Of The Following Equation E X 12e X 1 0 Youtube




Maclaurin Series Of Eˣ Video Khan Academy




Find A Real Root Of The Equation X E X Using The Newton Rapshon Method Mathematics 3 Question Answer Collection



Maclaurin Series Of Exponential Function
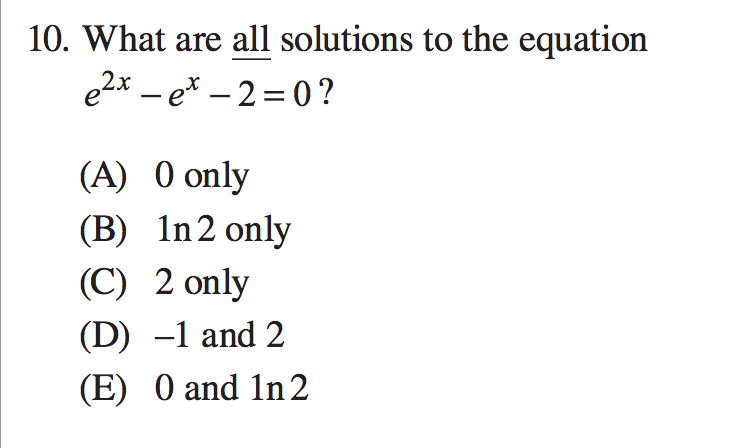



Solved What Are All Solutions To The Equation E 2x E X Chegg Com
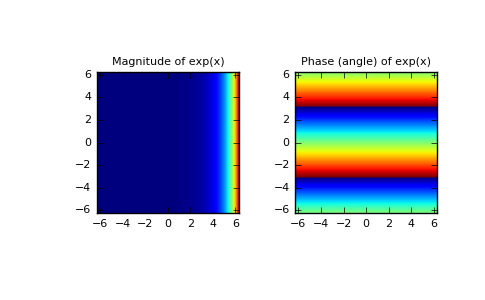



Numpy Exp Numpy V1 11 Manual
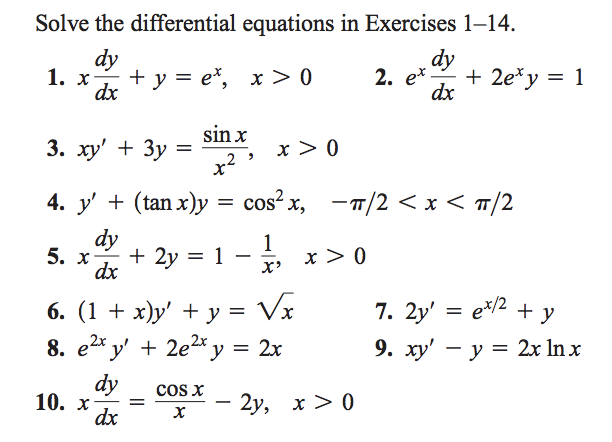



Solved Solve The Differential Equations In Exercises 1 14 Chegg Com



2




Taylor Polynomial For E X About X 0 Youtube
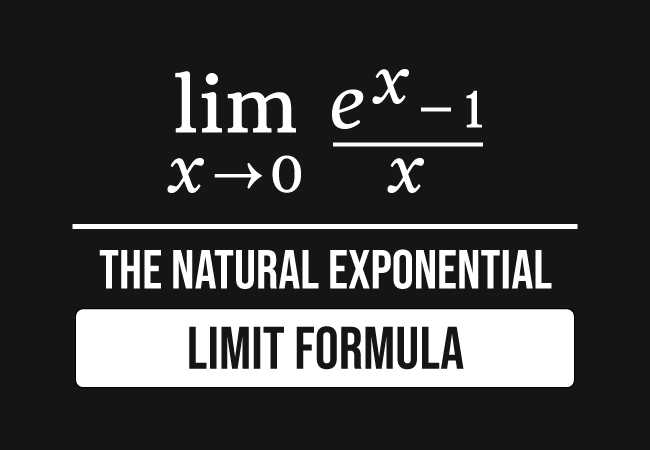



Lim X 0 E X 1 X Formula



Mathscene Exponentials And Logarithms Lesson 3




Summation Question E X Sum Of P X K From 0 To Inf The Student Room
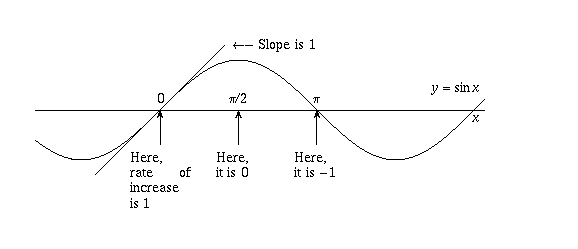



Question Corner Why Is E Pi I 1




How Do You Find The Equation Of The Tangent To The Curve Defined By Y 2e X 1 E X At The Point 0 1 Socratic



6 Derivative Of The Exponential Function



2



3



2
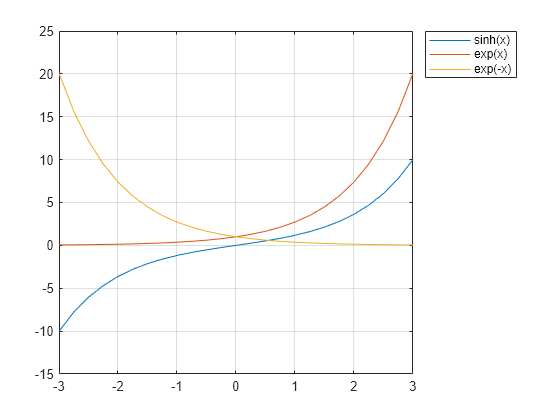



Hyperbolic Sine Matlab Sinh




Taylor Polynomial For E X About X 0 Youtube



2




Exponential Function Wikipedia



No comments:
Post a Comment