Solve by eliminnation methods 2x4y=5 2x4y=6 solve the system by elimination method 5x2y= 13 7x3y=17 Solve x64 Determine whether the given numbers are solutions of the inequality 8,10,18,3 y8>2y3 Solve by the Math How do I x=2 and y=1 Hi there, Here we will use elimination method to solve the given system of an equation We have, 3xy = 5equation 1 x2y=4equation 2 Note here we have unequal coefficient for both x and y So we will first make coefficient of either x or y equal Here we well make coefficient of y equal by multiplying equation 1 by 2, we get 6x2y=10equation 33x/4y/3=7/6 x/22y/3=5/3 Answer by jim_thompson5910() (Show Source) You can put this solution on YOUR website!
How To Solve For X And Y In X Y 5 And Xy 6 Quora
X-y=3 x/3 y/2=6 by elimination method
X-y=3 x/3 y/2=6 by elimination method-By solve, I assume you mean find values for x and y The values of x and y can be a lot of different numbers For instance, if x = 2, y = 15 beThese are the elimination method steps to solve simultaneous linear equations Let us take an example of two linear equations xy=8 and 2x3y=4 to understand it better Let, xy=8 ___ (1) and 2x3y=4 ___ (2) Step 1 To make the coefficients of x equal, multiply equation (1) by 2 and equation (2) by 1 We get,



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community
Solve this linear system using the elimination method 3x – y = 3 x y = 17 Good heavens, the y's are already lined up and signed up for us to eliminate them (3x x) (y y) = (3 17) 4x = x = 5 Plug x = 5 into the second original equation and solve for y 5 y = 17 y = 12 The solution seems to be (5, 12) Let's make a quick check for body doubles, evil clones, or demonicSolve for x and y using elimination method 10 x 3y = 75, 6x 5y = 11 Solve for x and y, using substitution method 2x y = 7, 4x 3y 1 =0 Solve the following system of equations by using the method of crossmultiplication 2x3y=17,quadCorrect answers 1 question xy=3 and X/3 y/2 = 6 Solve the following pair of linear equations by the elimination method and the substitution method
Elimination Method Steps Step 1 Firstly, multiply both the given equations by some suitable nonzero constants to make the coefficients of any one of the variables (either x or y) numerically equal Step 2 After that, add or subtract one equation from the other in such a way that one variable gets eliminatedNow, if you get an equation in one variable, go to Step 3Let's start by clearing those fractions The LCD for the first equation is 6, for the second equation is 15, so multiply both sides of these equations by those numbersSolve the Following Pair of Linear (Simultaneous ) Equation Using Method of Elimination by Substitution 2( X 3 ) 3( Y 5 ) = 0 5( X 1 ) 4( Y 4 ) = 0 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6
5 Solve this system of equations and comment on the nature of the solution using Gauss Elimination method x y z = 0 x – y 3z = 3 x – y – z = 2 a) Unique Solution b) No solution c) Infinitely many Solutions d) Finite solutions Answer b Clarification By Gauss Elimination method we add Row 1 and Row 3 to get the following matrix Equation 1 2x 3y = 8 Equation 2 3x 2y = 7 Step 1 Multiply each equation by a suitable number so that the two equations have the same leading coefficient An easy choice is to multiply Equation 1 by 3, the coefficient of x in Equation 2, and multiply Equation 2 by 2, the x coefficient in Equation 1By the process of elimination how do u solve 32xy=0 and 37y=10x asked in ALGEBRA 2 by homeworkhelp Mentor systemofequations;
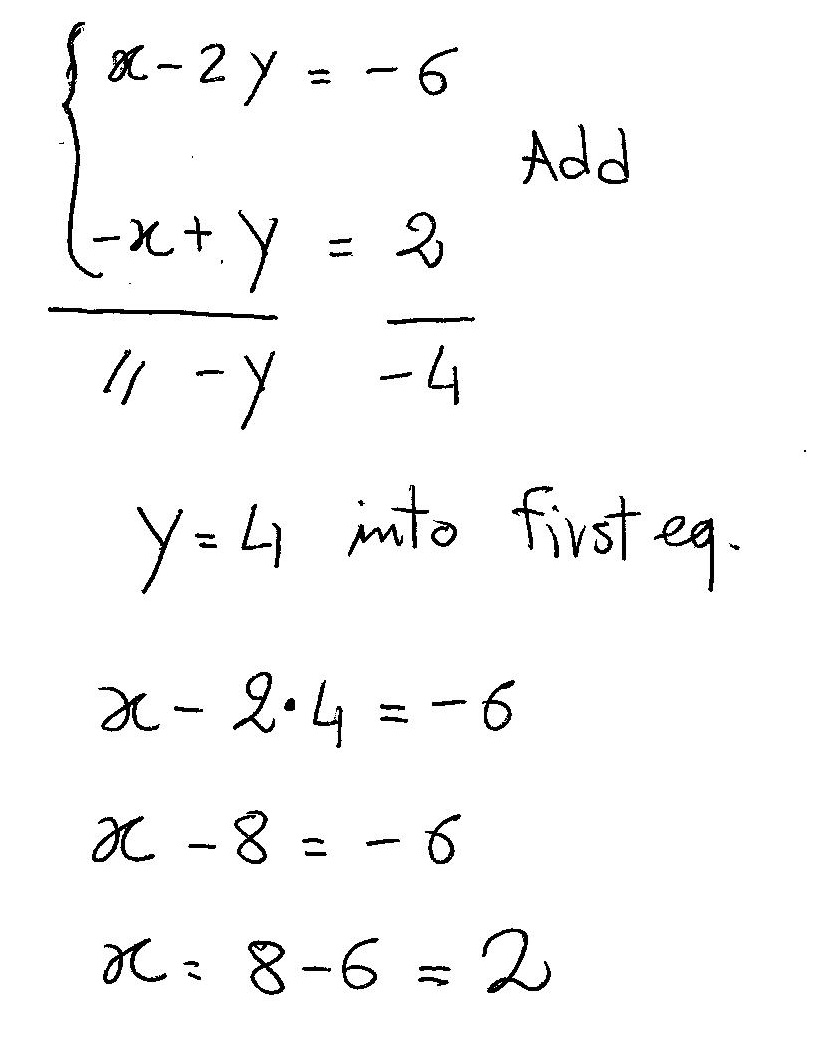



How Do You Solve X 2y 6 And X Y 2 Socratic
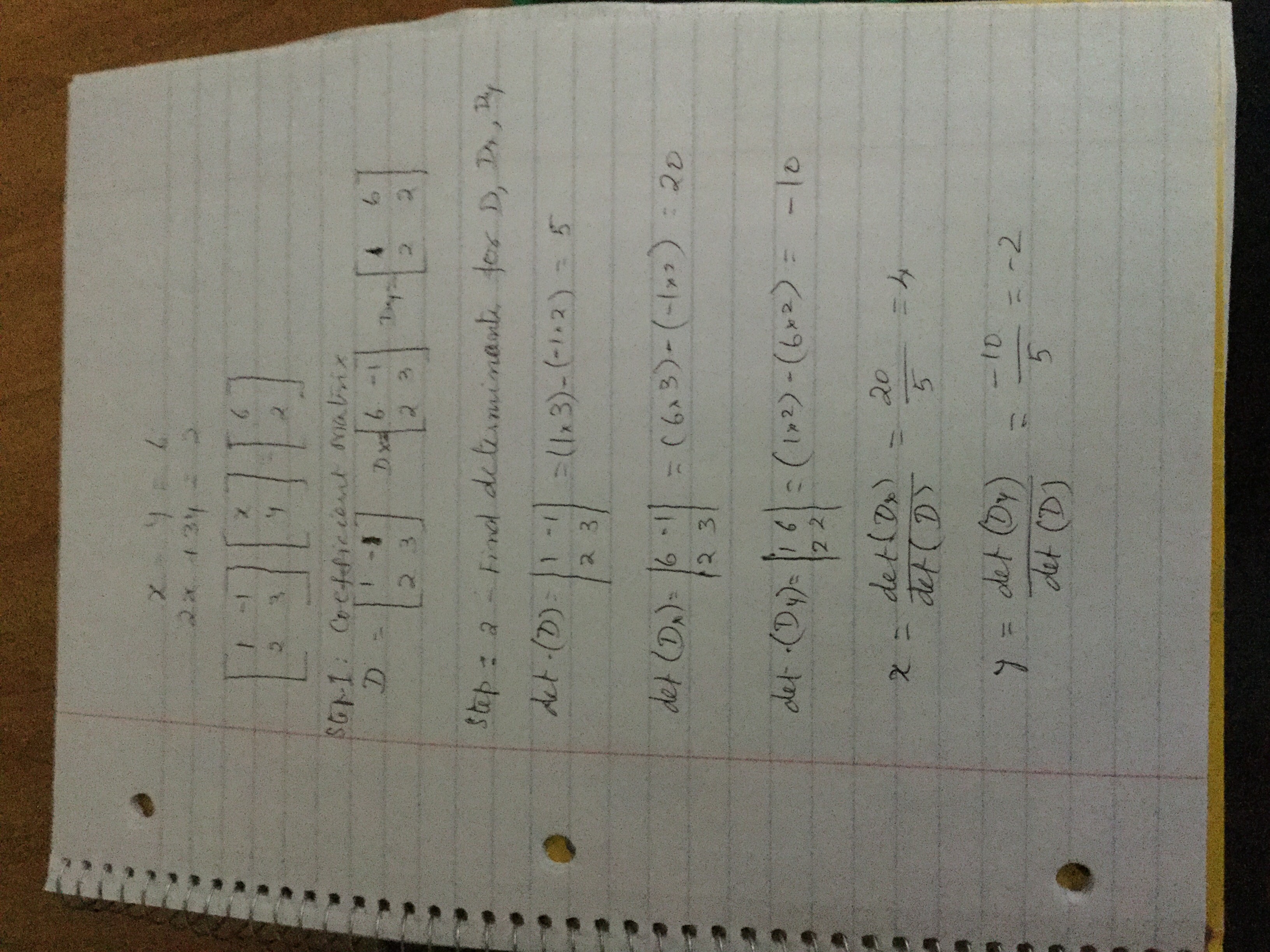



How Do You Solve X Y 6 And 2x 3y 2 Using Matrices Socratic
Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x 3y = 4 (ii) 3x 4y = 10 and 2x 2y = 2 (iii) 3x 5y 4 = 0 and 9x = 2y 7 (iv) x/2 2y/3 = 1 and xy/3 = 3 Get the answer to this question and access a vast question bank that is tailored for students`= x = 42/3 = 14` Hence, the solution of thee given system of equations is x = 14, y = 9 Concept Algebraic Methods of Solving a Pair of Linear Equations Substitution Method solve each system using the elimination method xy=6, 3xy=2 asked in ALGEBRA 1 by rockstar Apprentice eliminationmethod;



How To Solve This System Of Equations 3x 5y 6 2x 3y 4 Quora




Solve The Following Pair Of Linear Equations By The Elimination Method And The Substitution Method I X Y 5 And 2x 3y 4 Ii 2x 4y 10 And 2x 2y 2 Iii 3x 5y 4 0 And 9x 2y 7 Iv X 2 2y 3 1 And X Y 3 3
How do you solve x/2y/3=6 by elimination method to find the value of x and y of the following problem?Example 2 Solve by elimination {5 x − 3 y = − 1 3 x 2 y = 7 Solution We choose to eliminate the terms with variable y because the coefficients have different signs To do this, we first determine the least common multiple of the coefficients;Solve by Addition/Elimination xy=2 xy=4 x y = 2 x y = 2 x − y = 4 x y = 4 Multiply each equation by the value that makes the coefficients of x x opposite xy = 2 x y = 2 (−1)⋅(x −y) = (−1)(4) ( 1) ⋅ ( x y) = ( 1) ( 4) Simplify Tap for more steps Simplify ( − 1) ⋅ ( x − y) ( 1) ⋅ ( x y)




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube




Cramer S Rule To Solve A System Of 3 Linear Equations Example 2 Youtube
{eq}\displaystyle 3 x y = 2\\ 6 x 2 y = 4 {/eq} Elimination Method of Solving Equations When we are given two equations with two variables, it is called a system of equationsX/2y/9=6 x/7 y/3=5 by elimination methodSimplifying y 7 = 5(x 3) Reorder the terms 7 y = 5(x 3) Reorder the terms 7 y = 5(3 x) 7 y = (3 * 5 x * 5) 7 y = (15 5x) Solving 7 y = 15 5x Solving for variable 'y' Move all terms containing y to the left, all other terms to the right Add '7' to each side of the equation 7 7 y = 15 7 5x Combine likeIn this case, the LCM(3, 2) is 6




X Y 3 X 3 Y 2 6 Elimination Method Brainly In



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community
2 y = 3 y = 3/2 Hence the solution is (4, 3/2) Verification Applying the value of x and y in any one of the equations, we get x 2y = 7 x = 4 and y = 3/2 4 2(3/2) = 7 4 3 = 7 7 = 7 Question 2 Solve the following system of linear equations by elimination method 3x y = 8 , 5x ySolved by pluggable solver Solving a linear system of equations by subsitutionOr click the example About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding or



The Elimination Method



X Y 2
x=1 y=4 There are 3 ways to solve this Here is one way Elimination Line them up 2xy=6 xy=3 Add all that goes together 2xx=3x yy=0 63=3 Put it back into an equation 3x=3 x=1 Plug what x equals (1) into one of the previous equations (2•1)y=6 (2)y=62 y=4 or y=4 1y=3 (1) y=31 y=4Xy=5;x2y=7 Try it now Enter your equations separated by a comma in the box, and press Calculate!NCERT Solutions for Class 10 Maths Chapter 3 Exercise 34 Question 1 Summary On solving the pair of equations by the elimination method and the substitution method we get x, y as (i) x y = 5 and 2x 3y = 4 where, x = 19/5, y = 6/5 , (ii) 3x 4y = 10 and 2x 2y = 2 where, x = 2, y = 1 , (iii) 3x 5y 4 = 0 and 9x = 2y 7 where, x = 9/13, y = 5/13, (iv) x/2 2y/3 = 1 and x y/3



How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic




X 2 2y 3 1 And X Y 3 3 Solve By Elimination Method Brainly In
Click here👆to get an answer to your question ️ Solve equations using substitution method 2x y = 3 and 4x y = 3 Join / Login >> Class 10 >> Maths >> Pair of Linear Equations in Two Variables Solve equations using substitution method 2 x − y = 3 and 4 x y = 3 A5 Answers Sathish thangaraj answered Solve using Gauss Elimination method X 2Y Z = 6 2X Y 3Z = 12 3x 2Y 4Z = 17 Thank Writer Comment Blurt If the linear equation in two variables 2x –y = 2, 3y –4x = 2and px–3y = 2are concurrent, then find the value of p If ܽa b = 35 and a − b =
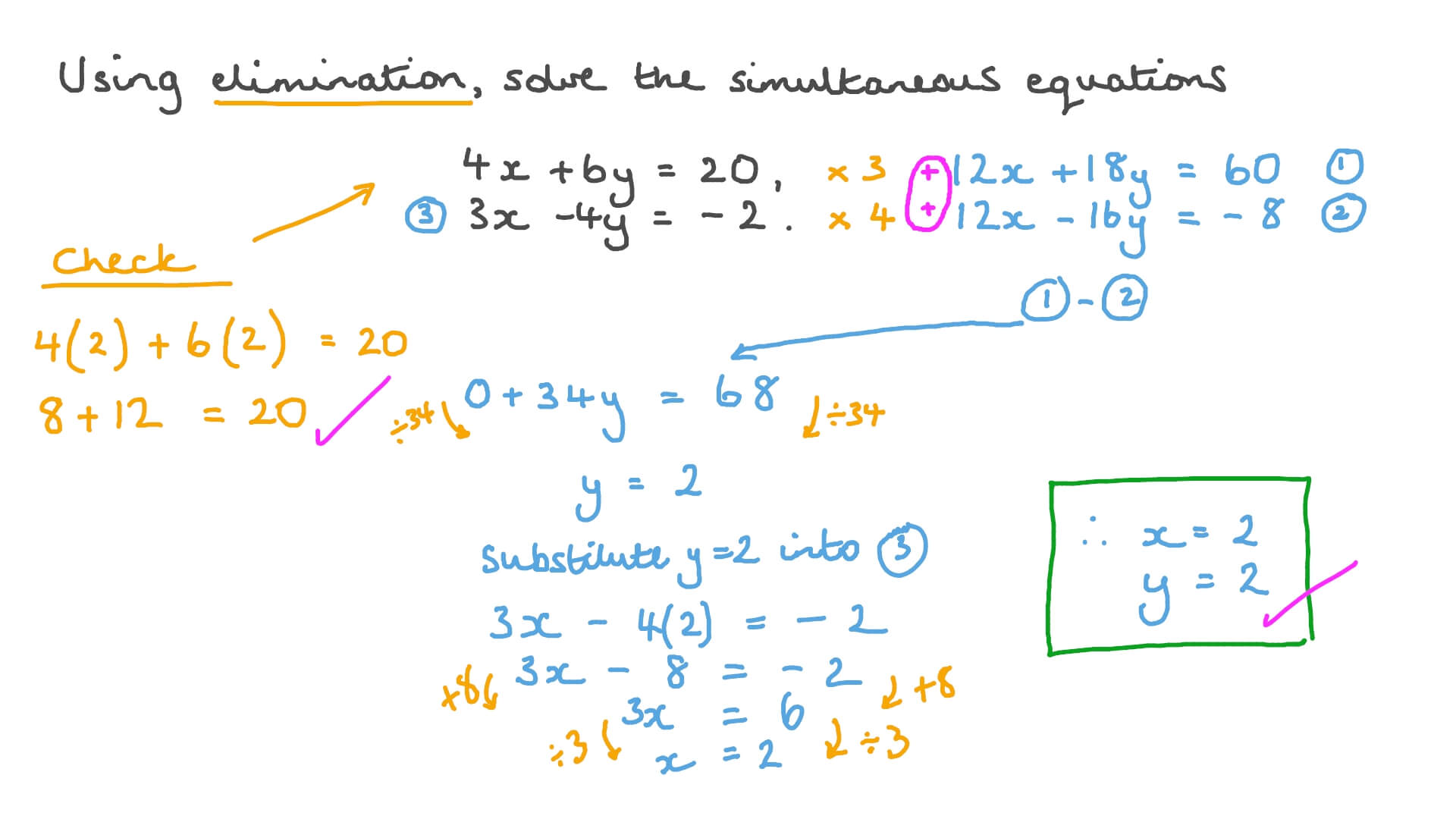



Question Video Solving Simultaneous Using Elimination Where Both Of The Equations Needs To Be Multiplied Nagwa



Solve The Following Pair Of Linear Equations By Substitution Method 3x 2y 7 0 4x Y 6 0 Sarthaks Econnect Largest Online Education Community
Transcript Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (iv) 𝑥/22𝑦/3=−1 𝑎𝑛𝑑 𝑥−𝑦/3=3 Given x/22y/3=−1 (3(x) 2(2y))/(2 × 3)=−1 (3𝑥 4y)/6=−1 3x 4y = −1 × 6 3x 4y = −6 x – y/3=3 (3𝑥 − 𝑦 )/3=3 3x – y = 3(3) 3x – y = 9 We use elimination method withFree system of equations elimination calculator solve system of equations unsing elimination method stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicySolve by Addition/Elimination x2y=3 2x3y=9 Multiply each equation by the value that makes the coefficients of opposite Simplify Tap for more steps Simplify Tap for more steps Apply the distributive property Multiply by Multiply by Add the two



1



Solve 5 X 1 1 Y 2 2 And 6 X 1 3 Y 2 1 Studyrankersonline
Click here👆to get an answer to your question ️ Solve the following pair of linear equations by the elimination method and the substitution method x2 2y3 = 1 and x y3 = 3Solve the Given equation in Elimination method and Substitution Method9x – 2(9) = 108 x = 14 Answer x = 14 and y = 9 ← Prev Question Next




Solved Solve The Following Pair Of Linear Equation By Substitution Method 3x 2y 7 0 4x Y 6 0




Solution Of X Y 3 And X 3 Y 2 6 By Elimination Method Brainly In
Question 4841 Solve the system by the addition method x/3y/2=5/6 x/5y/3=3/5 Answer by rapaljer (4671) ( Show Source ) You can put this solution on YOUR website! To eliminate x x in the second equation, multiply the first equation by −7 − 7 and add it to the second equation −7x − 21 2 y = 7 2 7x − 6y = 13 − 33 2 y = 33 2 − 7 x − 21 2 y = 7 2 7 x − 6 y = 13 − 33 2 y = 33 2 which leads to y = −1 y = − 1 To find the value for y y, substitute the value for x x into one of theHence, y = 2 Therefore, x = 1 and y = 2 is the solution of the set of equations 2x y = 4 and 5x – 3y = 1 Elimination Method Examples Take a look at the elimination method questions Example 1 Solve the following equations using the addition method 2x y = 9 3x – y = 16 Solution If you add down, the y variables will cancel out




Solved Find The Value Of X Y In The Equation X 3y 7 0 3x 3y 1 0 By The Method Of Elimination




Solve The System Using Gaussian Elimination Or Gauss Jordan Elimination 3x 3y 3z 30 9x 9y 9z 90 1 5x 1 5y 1 5z 15 Select One A 2 2 6 Ob X Y Z 1 3x 3y 3z 30 Os Solve The
Example 2 Solve the system using elimination Solution Look at the x coefficients Multiply the first equation by 4, to set up the xcoefficients to cancel Now we can find Take the value for y and substitute it back into either one of the original equations The solution is Example 3 Solve the system using elimination methodThe trick with Gaussian elimination is to find the leading element (circled) at from the starting matrix and new matrix at each step This will give us an upper triangular matrix in Row Echelon form Then we can reduce further down to Reduced RowElimination Method xy = 5 and 2x3y = 4For online Tuition's from me WhatsApp me on 91 LinkedIn Profilehttps//wwwlinkedincom/in/arunmamidi8b




Solving Systems Of Equations With Fractions Or Decimals Video Lessons Examples And Solutions



Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community
Ex 34, 1 (Elimination)Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving This leaves us with a linear equation with one variable that can be easily solved 2x = 6 x = 3 At this point, we have the x coordinate of the simultaneous solution, so all that is left to do is back substitute to find the corresponding y value x y = 5 3 y = 5 y = 2 The solution to the system is (3, 2)The elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6 = −6 and x y = 8, you can add x y to the left side of the first equation and add 8 to the right side of the equation And since x y = 8, you are adding the same value to each side of the first




Solved Solve 3x 4y 10 2x 2y 2 By The Method Of Elimination




Systems Of Equations Substitution Method Ppt Video Online Download
Solve the following pair of equations by the elimination method and the substitution method x/2 (2y)/3 = 1 and x y/3 = 3 Updated On 253 For the y, you can just plug x into one of the equations and solve I'll use the first one 63y=0 Now get the ys to one side 6=3y Divide both sides by 3 to get y= 2 Now that you have an x and a y coordinate, your solution is (6,2) To check plug both values in for their variables into each equationQuestion How would you solve this equation, by either using the substitution method or the elimination method?




Solved Solve For X And Y 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2




Chapter 5 Review Exercises
Solve for x and y x/2 – y/9 = 6, x/7 y/3 = 5 (2) Let us use elimination method to solve the given system of equations Multiply (2) by 3 And subtract both the equations From (1); Solve each of the following systems of equations by the method of crossmultiplication (xy)/xy = 2, (x y)/xy = 6 asked Apr 27 in Linear Equations by Gargi01 ( 506k points) pair of linear equations in two variables X/7y/3=5 x/2y/9=6 by elimination method 2 See answers Advertisement Advertisement akshatagile akshatagile The eqn are simplified and then eqn ii is multiplied with suitable coefficient Hope it helps tqsm Advertisement




Solve X Y 3 And X 3 Y 2 6 By Substituting Methos Scholr




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution




X Y 3 And X 3 Y 2 6 Solve The Following Pair Of Linear Equations By The Elimination Method And Brainly In



2x 3y 13 7x 2y




X Y 3 X 3 Y 2 6



Solve The Following Pairs Of Linear Equations By The Substitution Method 3x 2 5y 3 2 X 3 Y 2 13 6 Sarthaks Econnect Largest Online Education Community




Solve The Following Systems By Gaussian Elimination Chegg Com
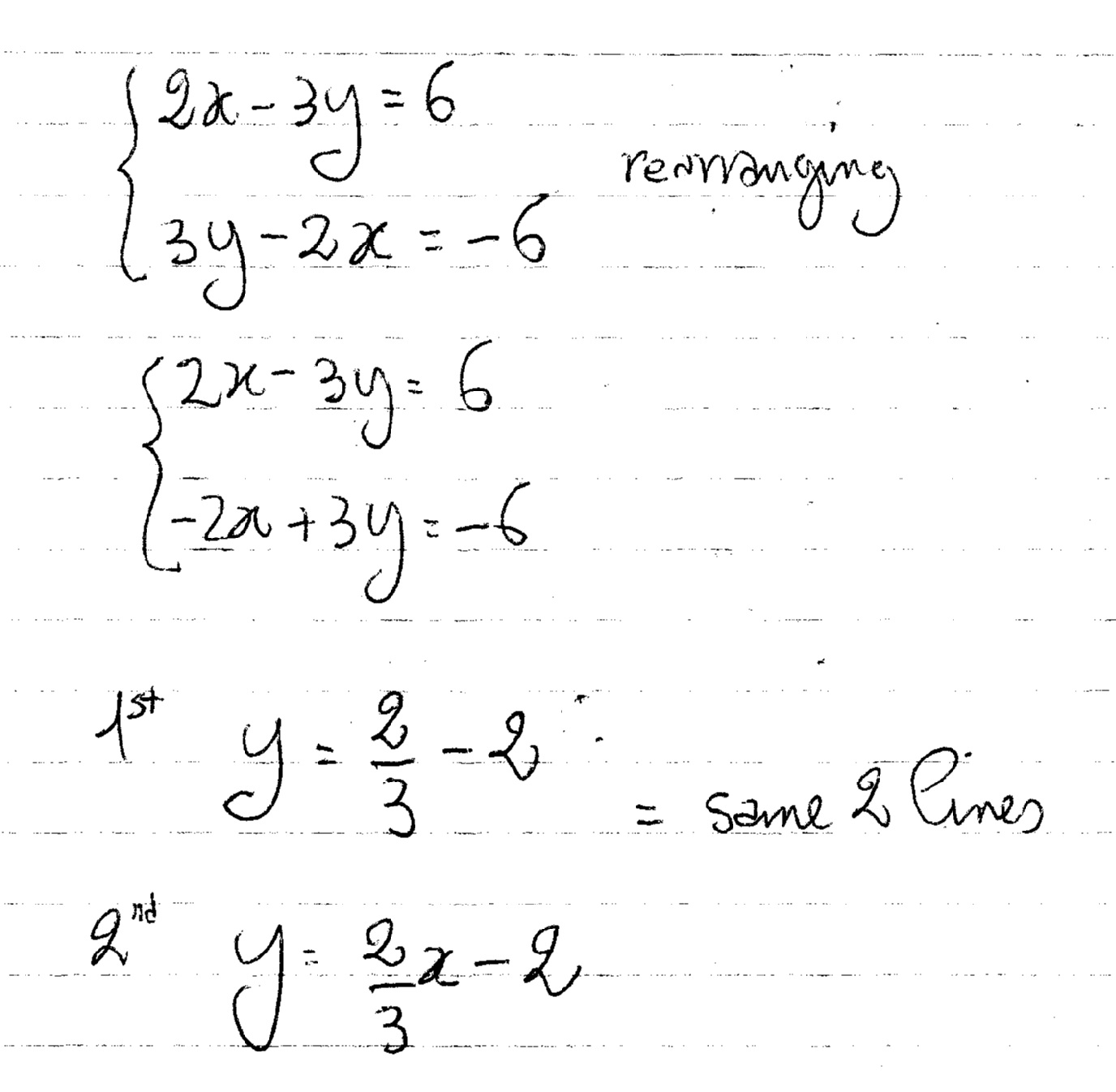



How Do You Solve The System Of Equations 2x 3y 6 And 3y 2x 6 Socratic



How To Solve For X And Y In X Y 5 And Xy 6 Quora




Let S Learn Solving Systems Using The Substitution Method
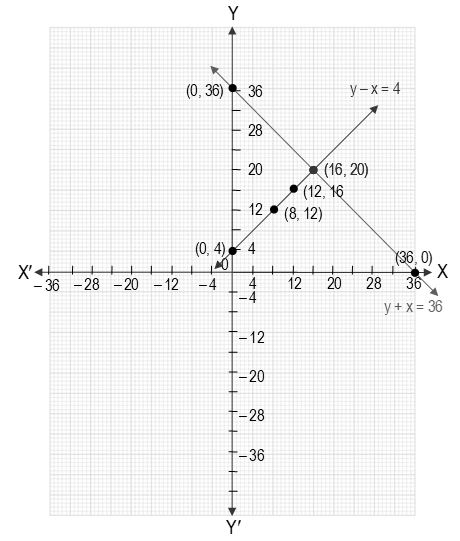



Pair Of Linear Equations In Two Variables




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




J19
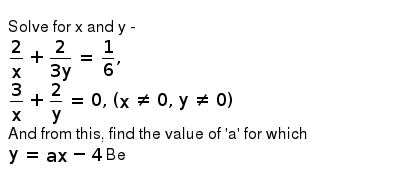



What Is The Value Of Y In The Equation 2 3y 6 0 2 0 2 6




Solving A System Of Equations Using A Matrix Precalculus Socratic




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15




Solve By Reducing Them To A Pair Of Linear Equations 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Youtube




3x 2 5y 3 2 X 3 Y 2 13 6 In Substitution Method Brainly In




5 3 Elimination Using Addition And Subtraction Ppt Download



Solved Find The Common Solution Of Each Using The Elimination Substitution And Graphical Method 2x Y 2 X 3y 36 2 3x Y 6 X Y 6 3 Course Hero



How To Solve The Simultaneous Equations X 2 Y 2 36 And X 2y 6 Quora



How To Transform The Linear Equations X Y Z 6 2x Y 2z 10 3x 3y 4z 21 In A Matrix Equation And Solve Them By Finding The Inverse Of Coefficient Matrix Using The Adjoint Method Quora




Systems Of Equations Substitution Method Ppt Video Online Download




Ex 3 6 1 Iii Iv 4 X 3y 14 3 X 4y 23 Ex 3 6



Www Mayfieldschools Org Downloads 3 3 solving systems by elimination answers Pdf
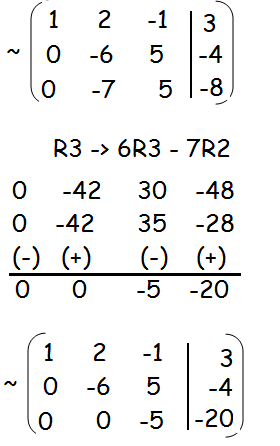



Solving Linear Equations Using Gaussian Elimination Method




2 3 6 7 1 Without Matrices Solve The Following System Using The Gaussian Elimination Method Homeworklib




X 2 2y 3 1 Amp X Y 3 3 Solve By Eliminations Or Substitution Method Brainly In
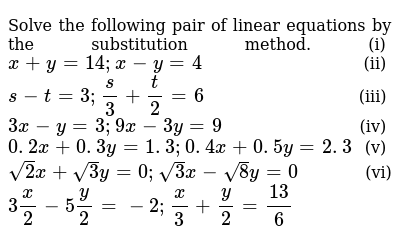



Solve The Following Pair Of Linear Equations By The Substitution Method I X Y 14 X Y 4 Ii S T 3 S 3 T 2 6 Iii 3x Y 3 9x 3y 9 Iv 0 2 X 0 3 Y 1 3 0 4 X 0 5 Y 2 3 V Sqrt 2 X Sqrt 3 Y 0 Sqrt 3 X Sqrt 8 Y 0 Vi 3x 2 5y 2 2 X 3 Y 2 13 6




Warm Up Solve Each Equation For X 1 Y X Y 3x 4 Ppt Video Online Download



Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf




6 2 Solving Systems Of Linear Equations 455 We Have Chegg Com




Consider The Following System Of Linear Equations X Chegg Com




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15
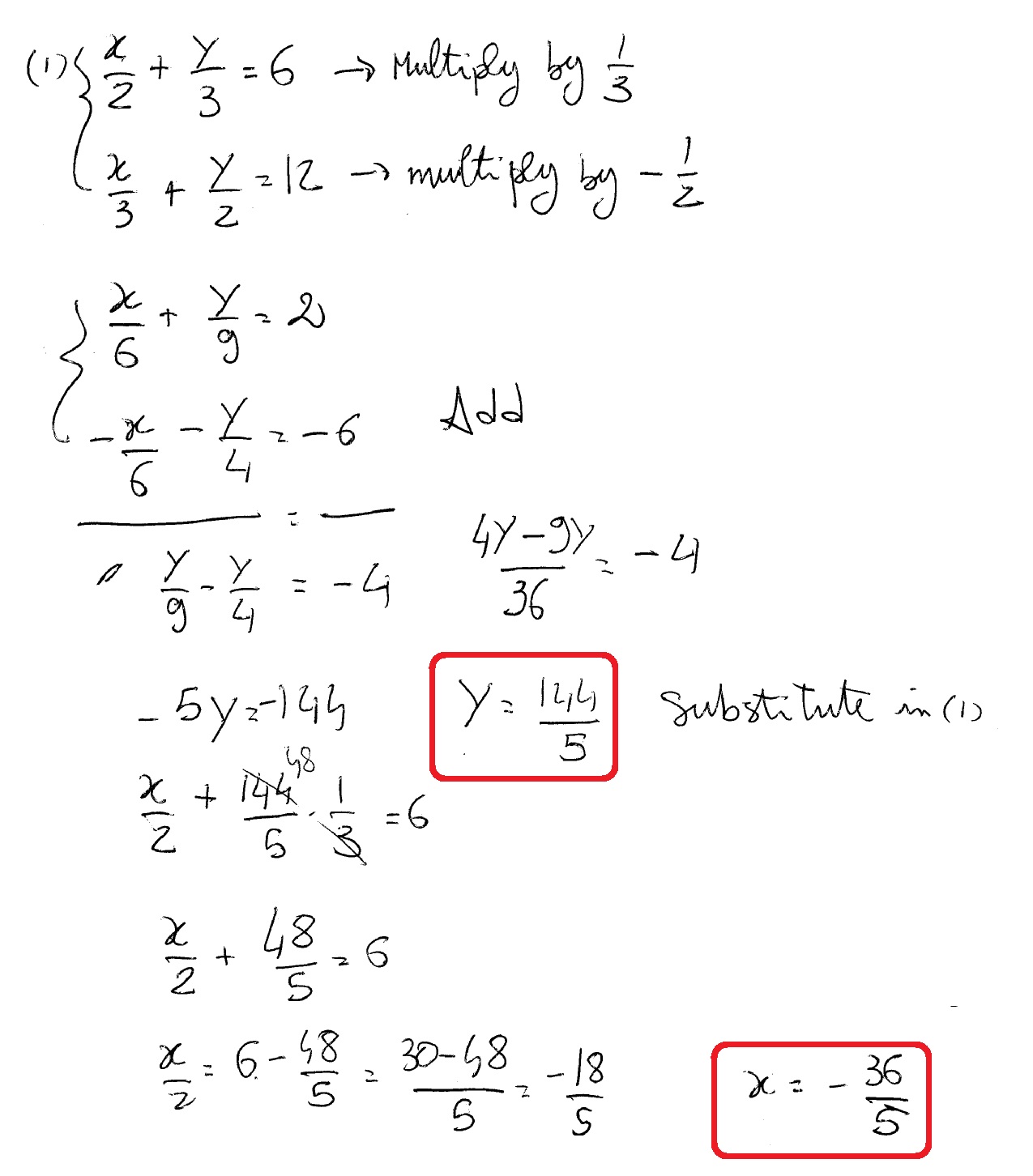



How Do You Solve X 2 Y 3 6 And X 3 Y 2 12 Socratic




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution



How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic




Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook




X 2 2y 3 1 X Y 3 3 Solve The Given Equation Using Elimination And Substitution Method Youtube




Solving Systems Of Linear Equations Using The Elimination Method




Solve The Following Pair Of Linear Equations By The Substitution Method 3x 2 5y 3 2x 3 Y 2 13 6 Brainly In




Example 12 Use Elimination Method 2x 3y 8 4x 6y 7




3 Systems Of Linear Equations



Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline




Solving Systems Of Equations With Fractions Or Decimals Video Lessons Examples And Solutions



2x 3y 0 3x 4y 5




Solved Solve For X And Y X 6y 6 3x 8y 5




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt




Ncert Solutions Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Ship Hang Nhanh




1 Topic The Substitution Method 2 Topic The Substitution Method California Standard 9 0 Students Solve A System Of Two Linear Equations Ppt Download




2 Use Cramer S Rule To Solve The Following Set Of Chegg Com




22 4 3x 6 317 3 2x 3y 11 4 X 2y 8 6 26 Chegg Com




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo




How Do You Solve The System 4x 2y 6 And X Y 3 Socratic




Algebra Ii




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube




Use The Substitution Method To Solve The System Of Equations Cho



Solve The Following Systems Of Linear Equations By Gaussian Elimination Method I 2x 2y 3z 2 X 2y Z 3 3x Y 2z 1 Sarthaks Econnect Largest Online Education Community




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula




Question 2 10 Points Each Solve Each Of The Chegg Com




𝙎𝙤𝙡𝙫𝙚 𝙗𝙮 𝙚𝙡𝙞𝙢𝙞𝙣𝙖𝙩𝙞𝙤𝙣 𝙨𝙪𝙗𝙨𝙩𝙞𝙩𝙪𝙩𝙞𝙤𝙣 𝙢𝙚𝙩𝙝𝙤𝙙 X 2 2y 3 1 X Y 3 3 𝘾𝙡𝙖𝙨𝙨 𝙓 𝙉𝙘𝙚𝙧𝙩 𝙈𝙖𝙩𝙝𝙨 𝙀𝙭 3 4 𝙌1 Iv Youtube




4 Given F X And G X Find F G X 5 8 X Chegg Com




Solved Solve The Following Systems Of Equations By The Method Of Cross Multiplication 5x Y 2x Y 1 15x Y 7x Y 10 Where X 0 Y 0 And X Y




Solved X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Brainly In



Systems Of Linear Equations




Graph Graph Inequalities With Step By Step Math Problem Solver




Solving A System Of Equations Using A Matrix Precalculus Socratic



Simultaneous Equations Gmat Math Study Guide




Systems Of Equations With Substitution 2y X 7 X Y 4 Video Khan Academy



Solve The Following Pairs Of Linear Equations By The Substitution Method 3x 2 5y 3 2 X 3 Y 2 13 6 Sarthaks Econnect Largest Online Education Community
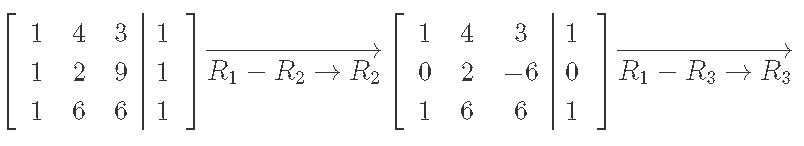



Systems Of Linear Equations Gaussian Elimination Studypug




X 3y 6 And 2x 3y 12 Solve Elimination Method Brainly In




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution




X Y 3 X 3 Y 2 6 Youtube




X Y 3 X 3 Y 2 6 Elimination Method Brainly In




2 X 2 3y 1 6 And 3 X 2 Y 0 Problem Set 1 Q6 1 Of Linear Equation In Two Variables Youtube




Solve The Following System Of Equations By Using The Method Of Elimination By Equating The Coefficients 3x 2y 11 2x 3y 4



No comments:
Post a Comment